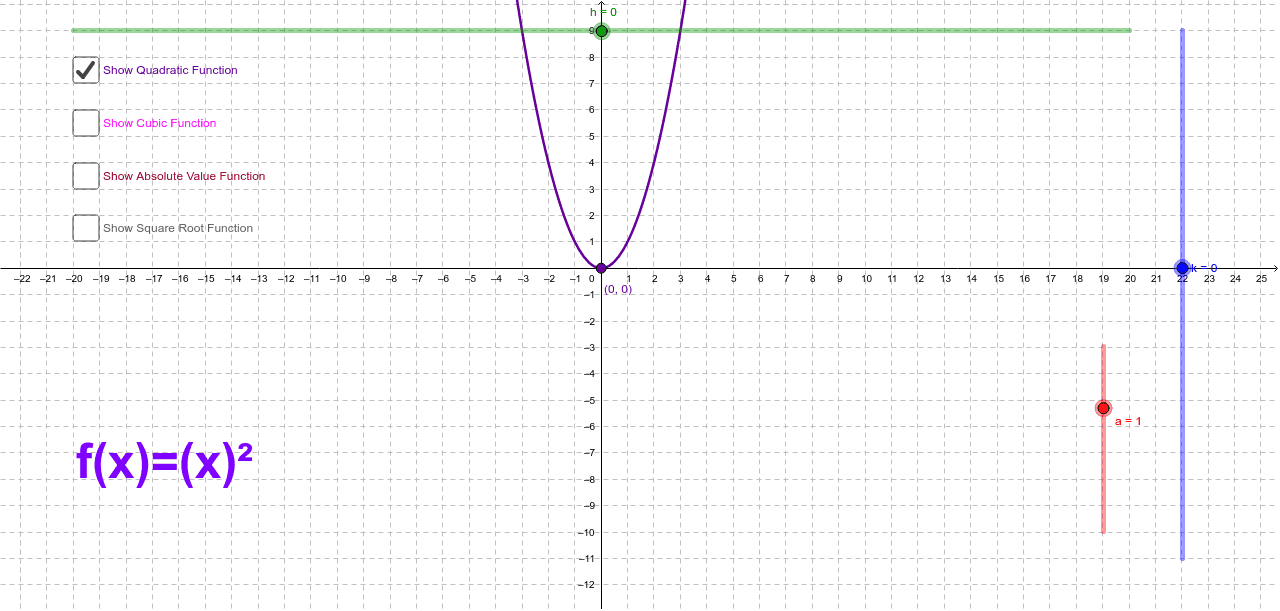
How does the graph of y = a(x h)2 k change if the value of h is doubled?Transformations of Qua dratic Graphs #1 What does a in y = a(x h)2 k do to th e graph? y=a(xh)^3k Author Lilach Explore the parent graph y=x^3 Experiment with the values of a, h, and k What happens to the graph as these values change?

23 Algebra 2 Unit 2 Linear And Absolute Value Interactive Notebook Family Function Outfit I Interactive Notebooks Absolute Value Notebook Gifts
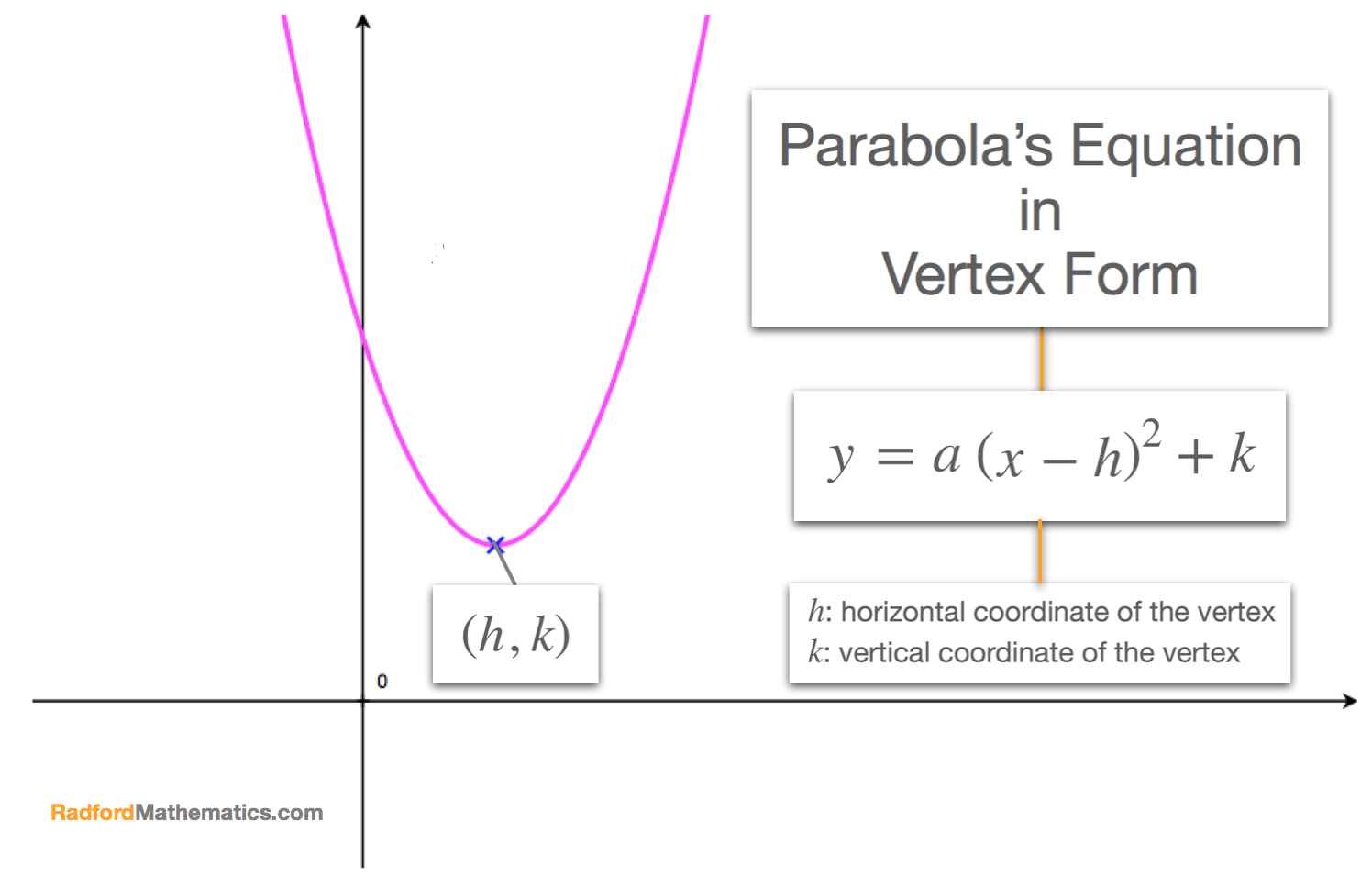
How to use y=a(x-h)^2+k
How to use y=a(x-h)^2+k-Role of k 2 Properties If k > 0, then the graph of y = a(x – h)2 k is translated vertically k units _____ o eg y = x 2 3; The graph of y = a (x – h)2 k change if the value of h is doubled It would be that the vertex of the parabola would move from h,k to 2h, k It is the vertex that is most affected, the rest would follow Hope this helps Have a nice day




Step Pattern And Mapping Notation Quadratics
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreTransformations of Qua dratic Graphs #3 What does h in y = a(x h)2 k do to th e graph?Video Notes Video Link
Why is it in vertex form of quadratic function y=a(xh) ^2k, getting value of h is opposite to its value?Video Notes Video LinkAll equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction ah^ {2}\left (2ax\right)hax^ {2}yk=0 a h 2 ( − 2 a x) h a x 2 − y k = 0
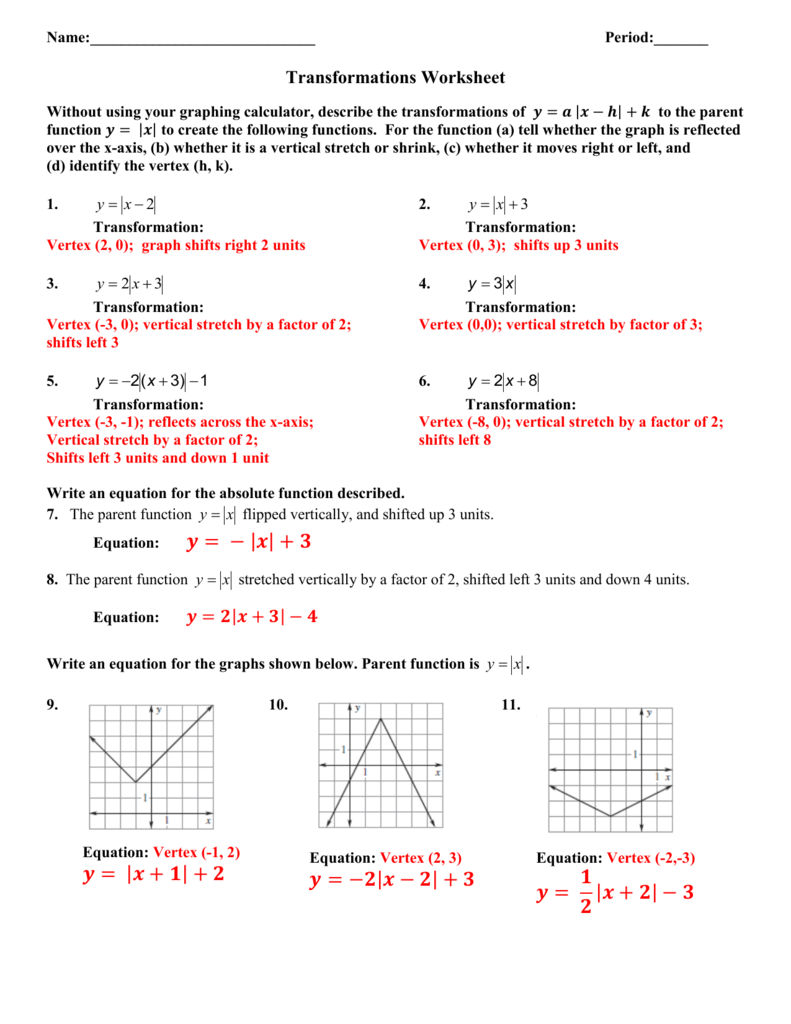
C a is positive B a is negative C a is the number zero _____ 8 If an absolute value function (ie y = a │x – h│ k) opens up, which isAnswer c) Graph the function using the equation in part a Explain why it is not necessary to plot points to graph when using y = a (x h) 2 k Show graph here Correct answers 1, question Transform each quadratic function into the form y=a(xh)^2k, then prepare a table of values and sketch its graph 1 y = 4x^2 4x 1 2 y = x^26



7th Section 8 4 Graphing F X A X H 2 K Youtube




Absolute Value Function
Video Notes Video LinkYou can put this solution on YOUR website!•Write quadratic functions in y = a(x h)2 k •transform graphs of functions into the equation y = a(x h)2 k •FIF8a, FBF3 Vertex Form y = a(x h)2 k Vertex Form y = a(x h)2 k



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora



Vertex Form
Explain the roles of a, h, and k in y = a(x – h )2 k, using the appropriate terminology to describe the transformations, and identify the vertex and the equation of the axis of symmetry;Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorTransformations Parent or Common Functions Identity y = x Absolute Value y = x Quadratic y = x2 Each of these functions above can have transformations applied to them A transformation is an alteration to a parent function's graph There are three types of transformations translations, reflections, and dilations



Absolute Value Transformations




Graphing Parabolas
B The 'h' B The 'k' C The 'a' D The 'x' _____ 7 If a quadratic function (ie y = a (x – h) 2 k) opens down, which is true?K in y = a(x – h)2 k Complete the following table Equation Value of a Value of h Value of k Vertex (h, k) # of x‐ intercepts Transformations starting from y = x2 Domain & Range y = 3(x – 2)2 1 a = 3 h = 2 k = 1 (2, 1) None • Vertical expansion by a factor of 3This video tutorial aims to help you in transforming quadratic functions from general form y = ax^2 bx c into vertex form y = a(xh)^2 k_____



Home Andrew Busch



Combination Of Transformations Notes Videos Qa And Tests Grade 10 Optional Mathematics Transformation Kullabs
Transform the quadratic function defined by y=ax2bxc into the form y=a(xh)2k 1Y=x26x3 2Y=5x2x5 Get the answers you need, now!Y = a (x h) 2 k The vertex of of the parabola is ( , ) The axis of symmetry is adirection of opening and vertical stretch or compression h horizontal translation k vertical translationVertex form tells of the transformations of the parent graph, which is y = x² a, is the dilation (a stretch and/or flip of the parent grap




6 2 Vertex Form




Answered Create A New Function In The Form Y Bartleby
SOLUTION Write each equation in the form y = a (xh)2 k y = 2x2 x 50 Practice!Y = a(x h) 2 k transformationsnotebook transformationsnotebook Graph of y = x2 x y transformationsnotebook A child kicks a soccer ball so that is barely clears a 2m fence TheNew Resources Fraction Addition;




Unit 1 Review Of Transformations Of A Graph F X Original Parent Graph Af X H K Transformed Graph A Value H Value K Value For Graphs Ppt Powerpoint




Quadratic Functions
Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download For more information and source, see on this link https//slideplayercom/slide// This video shows how to use vertex form ie y = a(x h)² k to graph a parabola or use it to write an equation from a graph This lesson was created fo Create a new function in the form \(y = a(xh)^2 k\) by performing the following transformations on \(f (x) = x^2\) Give the coordinates of the vertex for the new parabola g(x) is f (x) shifted right 7 units, stretched by a factor of 9, and then shifted down by 3 units g(x) = ?




Converting A Quadratic Function From Standard Form To Vertex Form Completing The Square Youtube




Standard Form To Vertex Form Calculator Mike S Calculators With Steps Free 21
0 In a quadratic(Circle your answer) a is positive a is negative a is the number zero 6 If a quadratic function (ie y = a(x – h)2 k) opens down, which statement below is true?4 Which parameter controls the opening in an absolute value (y = ax – h k) or a quadratic (y = a(x – h)2 k) function?



Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 718 10 14 abs value notes Pdf



1
Create a new function in the form \(y = a(x h)^2 k\) by performing the following transformations on \(f (x) = x^2\) Give the coordinates of the vertex for the new parabola h(x) is f (x) shifted right 3 units, stretched by a factor of 9, and shifted up by 7 unitsCoefficients of y = a(x – h)2 k Objectives In Chapters 2 and 3, you studied linear functions of the form f(x) = mx b A quadratic function is a function that can be written in the form of f(x) = a (x – h)2 k (a ≠ 0) In a quadratic function, the variable is always squared The table shows the linear and quadratic parent functionsY = a(x – h)2 k 1 yx 32 List the transformations?



Untitled Document




Quadratic Functions
The standard form of a quadratic function presents the function in the form f (x)= a(x−h)2 k f ( x) = a ( x − h) 2 k where (h, k) ( h, k) is the vertex Because the vertex appears in the standard form of the quadratic function, this form is also known as the vertex form of a quadratic function The standard form is useful for determining howPlay this game to review Mathematics What steps transform the graph y = x 2 to y = x 2 8 Preview this quiz on Quizizz Quiz Quadratic Transformations (a, h, and k) DRAFT 8th 12th grade Played 0 times 0% average accuracy Mathematics 43 minutes ago by woloshynYou can use transformations of quadratic functions to analyze changes in braking distance




Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1




How To Write Quadratic Functions Video Lesson Transcript Study Com
Vertex ( , ) x y x y 1 Determine the vertex and plot it8 2 Draw the axis of symmetry 3 Create an xytable, put your vertex in the MIDDLE, and label two points on either side 4 Draw a parabola through plotted pointsCoordinates of the vertex for the new parabola are x=?5 If a quadratic function (ie y = a(x – h)2 k) opens up, which statement below is true?




Quadratic Functions



How To Find Equations For Exponential Functions Studypug
Transform each equation from y = ax 2 bx c to y = a(x – h) k form 4) 2y = x – 8x 15 5) y = x2 2x – 35 6) y = 5x2 x 15 7) y = 2x2 2 x 42 28) y = x – 16x 28 9) y = x – 8x 12 10) 2y = 3x 18x – 21 11) y = 7x2 14x 21 12) y = x2 – 10x 21 13) 2y = x2 2– 14x 13 14) y = x – 12x 11 15) y = 9x 18x Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeK = _____ Relation to the Vertex The value of k is the _____




23 Algebra 2 Unit 2 Linear And Absolute Value Interactive Notebook Family Function Outfit I Interactive Notebooks Absolute Value Notebook Gifts



Www Youcubed Org Downloadable Diarra Lesson Plan
The vertex of the graph moves to a point twice as far from the xaxis The vertex of the graph moves to a point twice as far from the yaxis The vertex of the graph moves to a point half as far from the xaxisWag the dog Harmonic Oscillator;K = _____ If k < 0, then the graph of y = a(x – h)2 k is translated vertically k units _____ o 2eg y = x – 3;
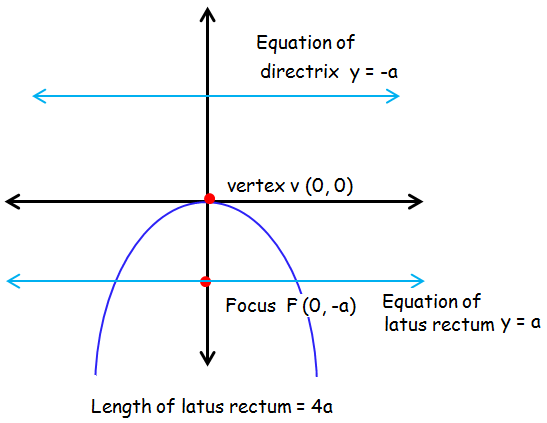



Parabola Formulas




Explaining A And H When You Have Y A X H 2 Youtube
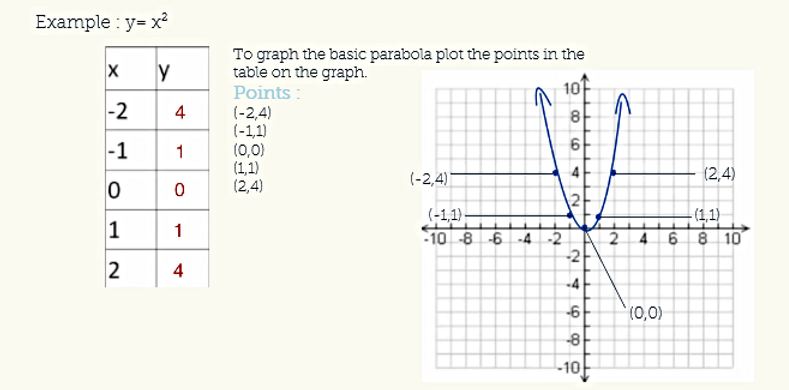
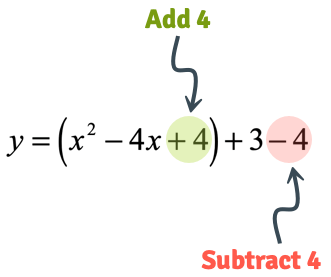
Take half of the x coefficient to get (ie ) Now add and subtract this value inside the parenthesis Doing both the additionThis video will demonstrate how to transform quadratic function from standard form to vertex form (y = a(x h)^2 k)#Quadratic Function#Vertex Form Vertex form y=a(xh)^2k All parabolas are the result of various transformations being applied to a base or "mother" parabola This base parabola has the formula y=x^2, and represents what a parabola looks like without any transformations being applied to it The table of values for a base parabola look like this



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf
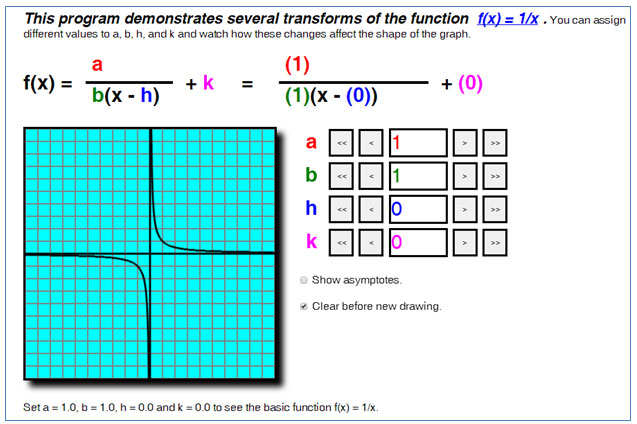



Transformations Of Square Root And Rational Functions Texas Gateway
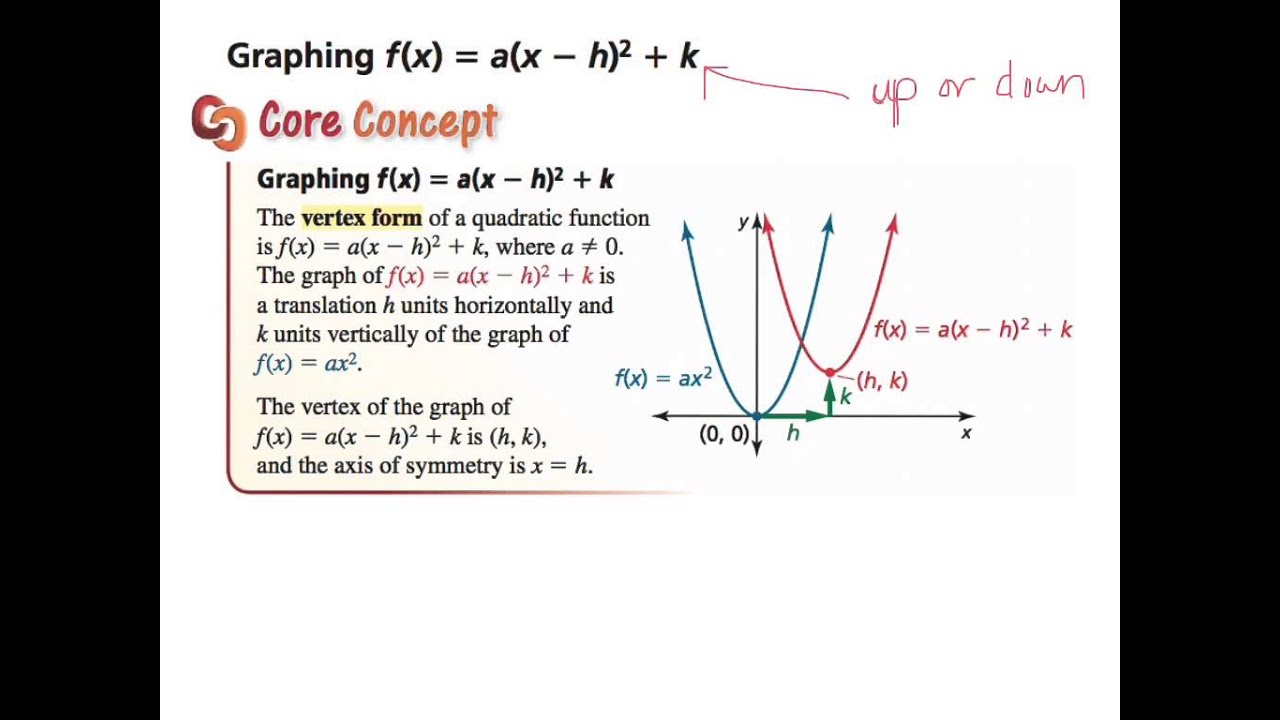
Quadratic equation y x² into y a x h 5 1 Using Transformations to Graph Quadratic Functions April 21st, 19 5 1 Using Transformations to Graph Quadratic Functions 315 In Chapters 2 and 3 you studied linear functions of the form f x mx b A quadratic function is a function that can be written in the form f x a x h 2 k a ?Notes 21 Using Transformations to Graph Quadratic Functions Objectives Transform quadratic functions Describe the effects of changes in the coefficients of y = a(x h)2 k Why learn this?K In this lesson you will learn about graphs of equations of the form y = a ( x − h) 2 k For example, you will look at equations such as y = 3 x 2, y = − 2 x 2, and y = 2 ( x 1) 2 3, and compare them to y = x 2 You will also learn about roots of quadratic equations and how the values of a, h, and k affect the number of roots
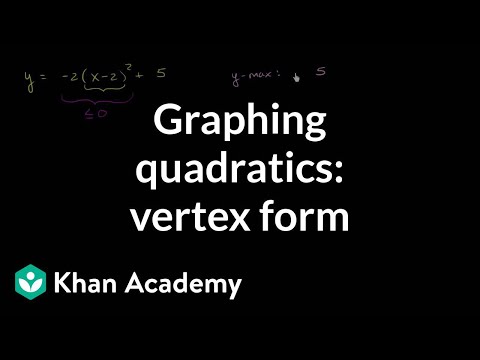



Graphing Quadratics Vertex Form Algebra Video Khan Academy



Vertex Form Quirky Quadratics
A) Put the function in the form y = a(x h)2 k Answer Show work in this space b) What is the equation for the line of symmetry for the graph of this function?Pythagoras' Theorem Area dissection 244 graph of y=a(xh)2k (part 1)notebook 4 Mar 71059 AM x y y = 2x2 5 Mar 76 AM The graph of y=x2 is reflected in the xaxis, compressed vertically by a factor of 1/4 , translated 1 unit to the left, and 2 units down Write the equation of this parabola y = a(x h)2 k 4




Parabolas In Standard Intercept And Vertex Form Video Lesson Transcript Study Com



When You Use The Vertex Form Y A X H 2 K What Information Do You Get From A Vertex Form Quora
Sketch, by hand, the graph of y = a(x – h )2 k by applying Transformations to the graph of y = x2Vertex ( , ) 2 yx 52 List the transformations?Transformations are the key to graphing and explaining where the parabola is It is only used in vertex form because each letter except x and y represents a transformation in this equation y=a (xh)^2k h = the vertex of the parabola will move to the right or left side of the graph



Graphing Quadratic Functions




Vertex Form Quadratics
Demonstrating understanding of the roles of a, h & k in y = a(x – h)2 k Using Vertex Form A Gizmo, complete the following Equation a h k Vertex (h, k) Transformations Starting from y=x2 Domain & Range y = 3(x 2)2 1 a = 3 h = 2 k = 1 (2, 1) •Vertical stretch by a factor of 3 •Translated 2 units right •Translated 1 unit upwards D {xx ∈ }43 transformations investigation day 2 1 y = a(x h)2 k Vertex Form k vertical translation 'k' units k > 0 , the graph is translated 'k' units up The graph of y = a (x – h)2 k change if the value of h is doubled It would be that the vertex of the parabola would move from h,k to 2h, k It is the vertex that is most affected, the rest would follow Hope this helps Have a nice day The vertex of the graph moves to a point twice as far from the xaxis




Ppt Investigating The Effect Of A H And K In Vertex Form Powerpoint Presentation Id




Lesson Effects Of Changing A H And K In The Graph Of Quadratic Functi
Transformations of Qua dratic Graphs #2 What does k in y = a(x h)2 k do to th e graph?Y=a(xh)^2k Which equation is equivalent to the formula below To convert a quadratic from y ax2 bx c form to vertex form y a x – h 2 k you use the process of completing the square Check how easy it is and learn it for the future For an organized list



Www Jensenmath Ca 4 4 part 1 lesson solutions Pdf
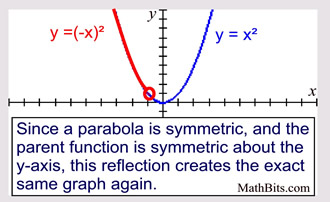



Parabola Parent Function Mathbitsnotebook A1 Ccss Math
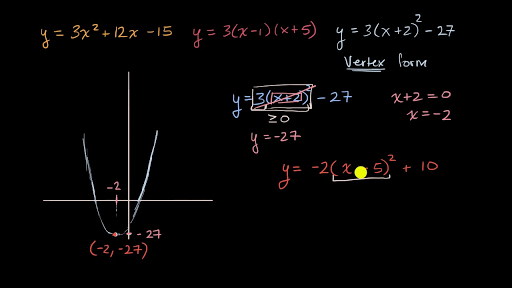



Vertex Form Introduction Video Khan Academy




Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download
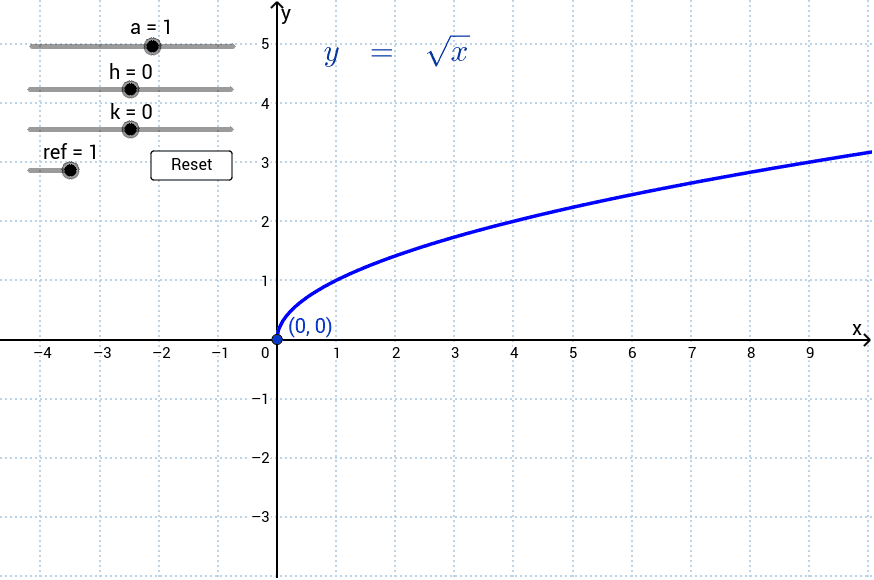



Transformations Of The Graph Y Sqrt X Geogebra
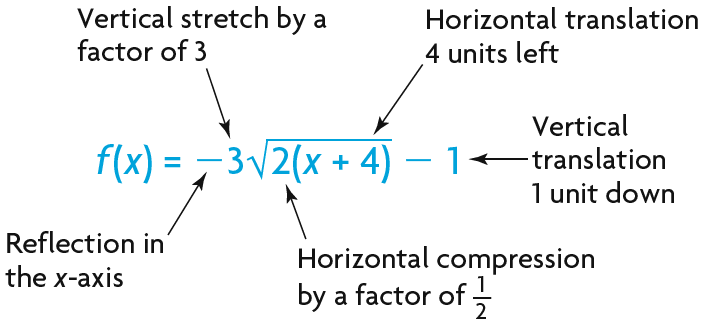



Using Transformations To Graph Functions Of The Form



Transforming Exponential Functions
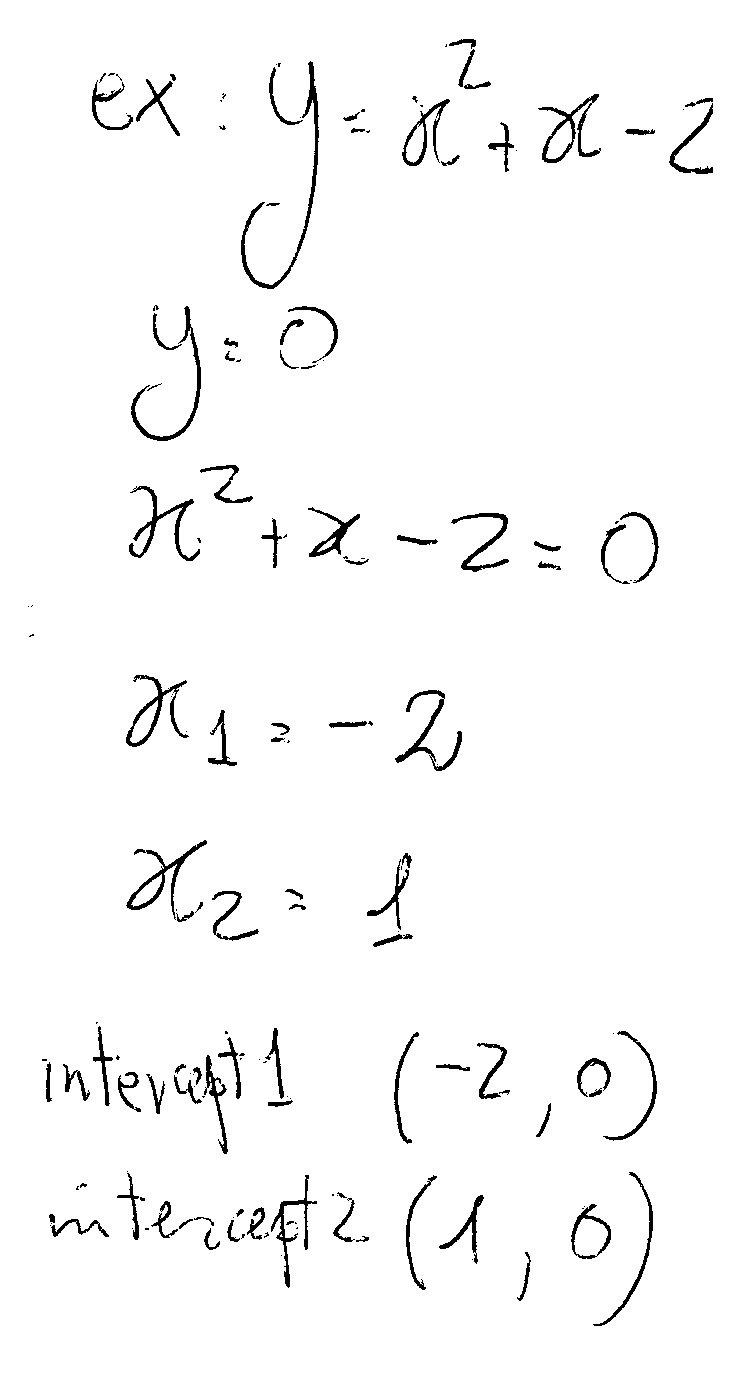



Quadratic Functions And Their Graphs Algebra Socratic




Vertex Form Quadratics




Step Pattern And Mapping Notation Quadratics




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube




Section 5 3 Transforming Parabolas Standard Form Vs Vertex Form Standard Form Is Y Ax 2 Bx C Vertex Form Is Y A X H 2 K Ppt Download
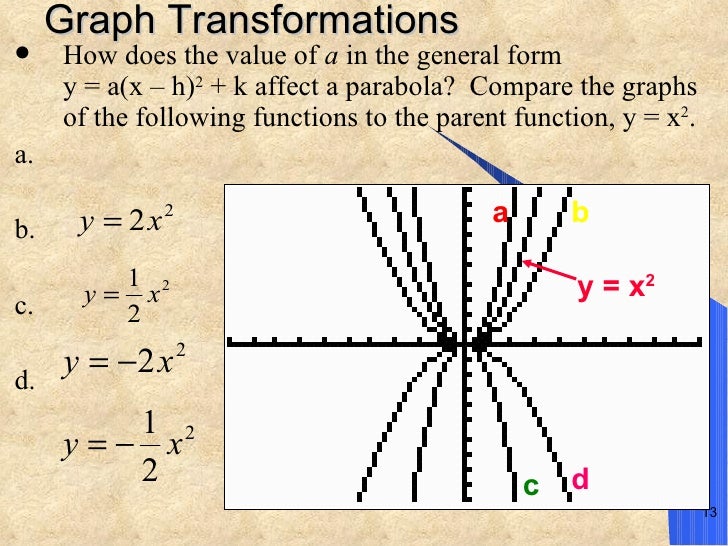



6 6 Analyzing Graphs Of Quadratic Functions



Www Npsk12 Com Cms Lib Va Centricity Domain 4555 Algebra ii lip 4 Pdf




X H 3 Formula Novocom Top



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora




Chapter 4 Part 1 Notes




Objective Connect Transformations Of Parabolas With Their Equations In Graphing Form Hw Check Correct In Red The Same But Different Packet In Ppt Download



Http Www Math Wsu Edu Faculty Dzhang 1fall14 1lecturenotes Fall14 Wed9 10 Pdf




Vertex Form Quadratics




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id
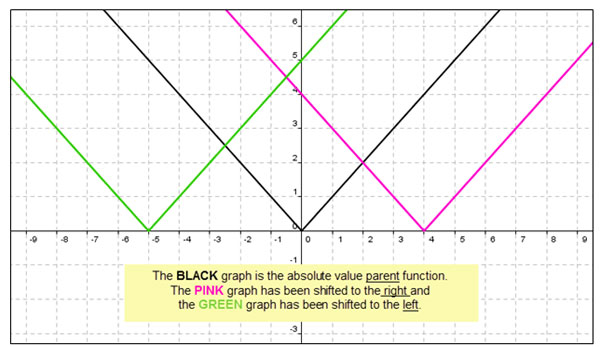



Transformations Of Absolute Value Functions Texas Gateway
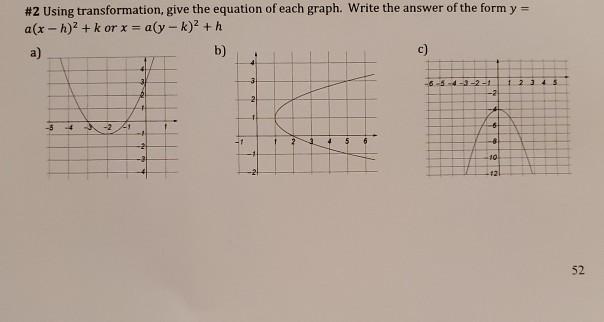



Solved 2 Using Transformation Give The Equation Of Each Chegg Com



Www Hackensackschools Org Site Handlers Filedownload Ashx Moduleinstanceid 1615 Dataid Filename Vertex form transformations notes day 1 Pdf



Staffweb Psdschools Org Eharding Alg1v Bigideasch 8 A1v8 4notesgraphingf A Xh K Pdf




X H 2 Y K 2 R 2 Examples Novocom Top




Transforming Quadratic Function In The Form Y A X H 2 K Graph Table Of Values Vertex Form Youtube



Search Q Vertical Stretch Tbm Isch
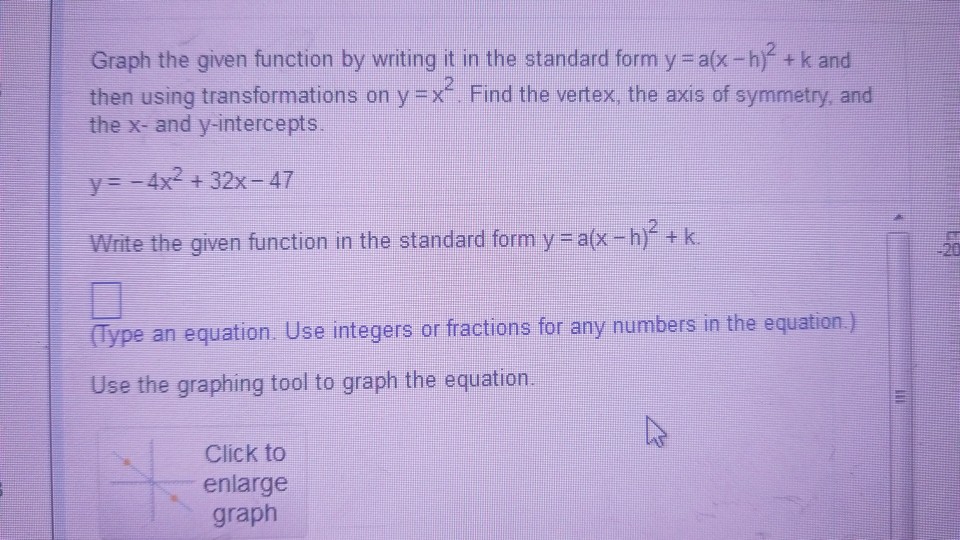



Solved Graph The Given Function By Writing It In The Stan Chegg Com



Vertex Form How To Find The Equation Of A Parabola




Finding Features Of Quadratic Functions Video Khan Academy




2 4 Use Absolute Value Functions And Transformations Ppt Video Online Download



Transformations Of Graphs A H K Geogebra



Www Caraleemath Com Uploads 2 8 4 0 Section 1 5 Order Of Transformations And Summary Pdf



Www Waynesville K12 Mo Us Cms Lib07 Mo Centricity Domain 718 10 14 abs value notes Pdf




Unit 1 Review Of Transformations Of A Graph F X Original Parent Graph Af X H K Transformed Graph A Value H Value K Value For Graphs Ppt Powerpoint




Unit 1 Review Of Transformations Of A Graph F X Original Parent Graph Af X H K Transformed Graph A Value H Value K Value For Graphs Ppt Powerpoint




Horizontal And Vertical Graph Transformations Examples Solutions Videos Worksheets Games Activities



Vertex Form Quadratics



Vertex Form Quirky Quadratics




Conic Sections 11 1 Parabola Conic Sections Parabola




Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download



Il Schoolwires Net Cms Lib Il Centricity Domain 330 10 1 graph absolute value and quadratic equations in vertex form notes Pdf
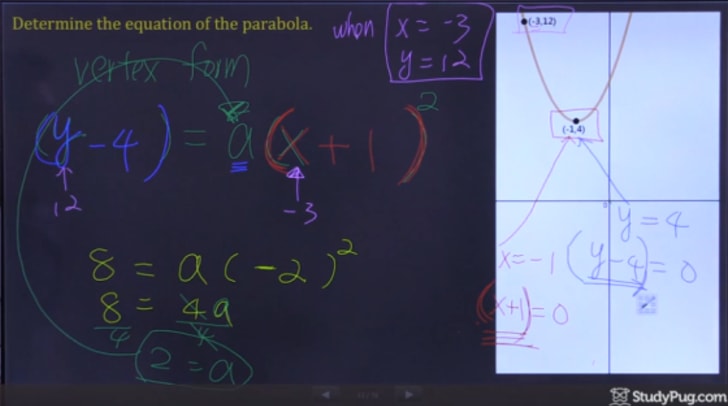



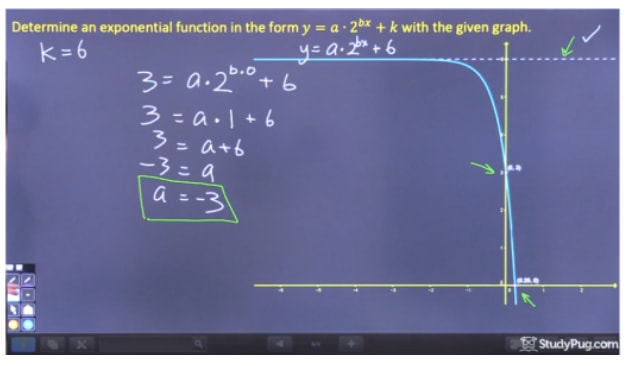
Finding A Quadratic Function With A Parabola Studypug
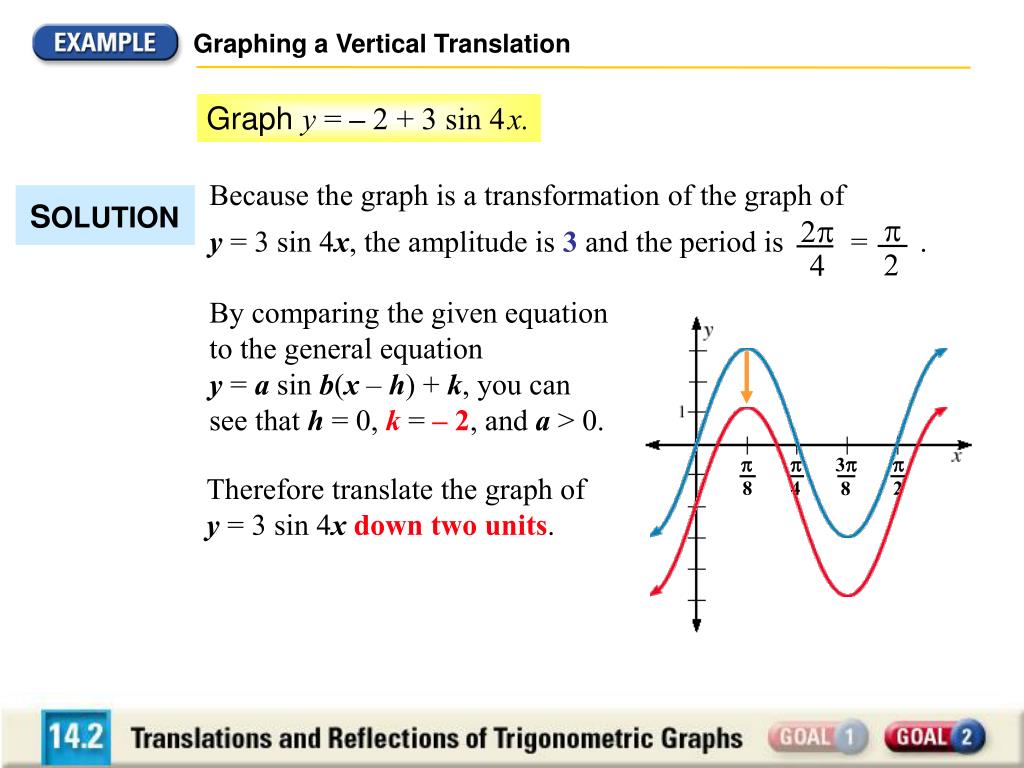



Ppt 4 3 Vertical And Horizontal Translations Powerpoint Presentation Id
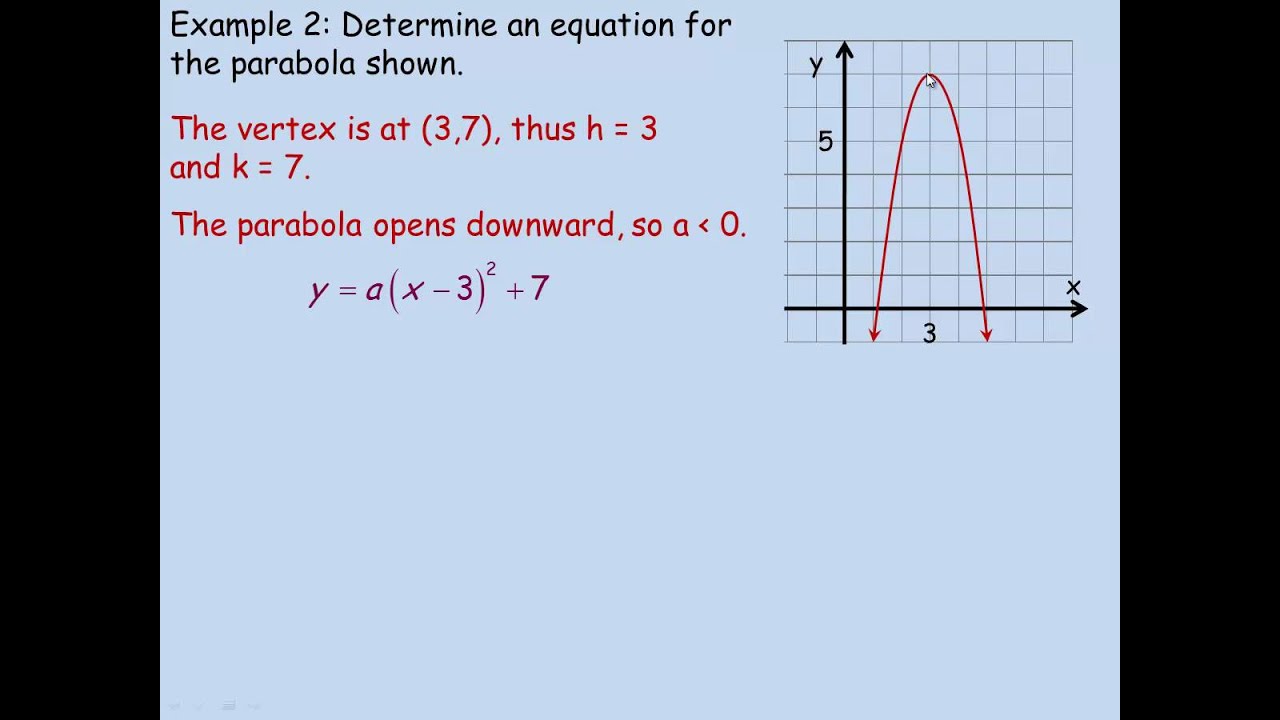



Graphing Y A X H K Youtube




Quadratic Functions




Writing Standard Form Equations For Parabolas Definition Explanation Video Lesson Transcript Study Com



Www Hackensackschools Org Site Handlers Filedownload Ashx Moduleinstanceid 1615 Dataid Filename Vertex form transformations notes day 1 Pdf




Graphing Parabolas




Graphing The Transformation Y F X H Concept Precalculus Video By Brightstorm
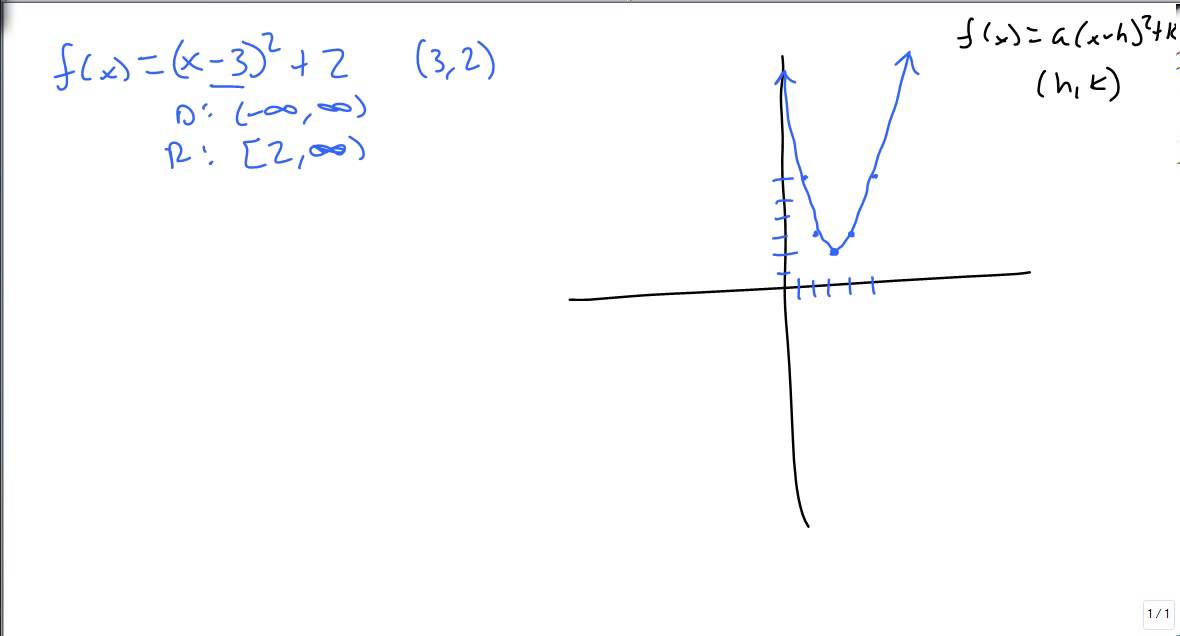



Graph By Transformations F X A X H 2 K Youtube




Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download




28 Algebra 2 Unit 2 Linear And Absolute Value Interactive Notebook Family Function Outfit W In Interactive Notebooks Absolute Value Notebook Gifts
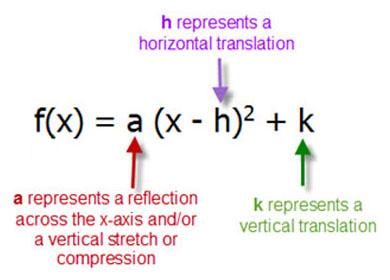



Untitled Document



Search Q Quadratic Formula Tbm Isch



Vertex Form Calculator




Transformations Of Parabolic Functions Algebra Ii




Y A X H 2 K Chegg Com




2 7 Absolute Value Functions And Graphs Ppt Download



Vertex Form Quirky Quadratics



Http Gelendonmath30p Pbworks Com W File Fetch Combinations




Ppt Quadratics Of The Form Y A X H 2 K Powerpoint Presentation Id




Quadratic Function



Completing The Square Step By Step Chilimath




Quadratic Functions



When You Use The Vertex Form Y A X H 2 K What Information Do You Get From A Vertex Form Quora



Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download



0 件のコメント:
コメントを投稿